中性子物質材料科学研究室のHPです。


推薦参考書
|
結晶の空間群と物性研究のための群論を勉強するには下の参考書を強くお勧めします。 「物質の対称性と群論」:今野豊彦著(共立出版) 4300円 ISBN4-320-03409-0 対称操作、点群、空間群の説明を豊富な具体例で解説してくれます。 さらに、群論が便利な道具であること、群論を使う事で、固体物理、化学の主要問題が手品のように簡単に扱えてしまうこと、を示す事に重点を置いていて、配位子場理論、分子軌道、フォノン、バンド理論などでの群論の役割を、大量の問題を使って丁寧に説明してくれています。 練習問題の配置もよく配慮されていて、たった今勉強したことを実際に使ってみる事ができます。練習問題を解いてみたくなる教科書です。 International Tableを使えるように成りたい人にもお勧めできます。 抽象論をさけ、物性研究への応用に重点をおいて現実の結晶、分子を使って段階を踏んで説明してくれているので、数式が苦手でも大丈夫です。しかも、途中で挫折したとしても、そこまでに読んだ情報がかならず役にたつでしょう。 わかりやすいだけでなくおもしろいので、私も第1章から順に問題を解き倒しています。おかげで最近、量子力学が分かった気になってきました。 これはお勧めします。やらないのはもったいない!! お勧め教科書をもうひとつ 「Space Groups for Solid State Scientists」 by G. Burns and A.M. Glazer (ISBN 0-12-145761-3) タイトルどおり、結晶学を基本に物性研究者の実際に役に立つように、空間群を基礎から説明してくれています。ひとつひとつの空間群、点群、結晶構造について豊富に実例を示して説明するので、抽象論になりがちな対称性の議論をイメージしやすくなっています。 たとえば、Fm3mを説明するのは次のような具合。 Cuの結晶構造(単純なFCC)を示し、<111>の3回軸、<100>, <110>に鏡映面があるからこの空間群はFm3m、と解説し、さらに一見異なる結晶構造に見えるNaCl, CaF2の結晶構造の図を示して、それが同じFm3mである事を解説します。さらにInternational TableのFm3mのページを示して、Cu, NaCl, CaF2のそれぞれの構造がどんな性質をもっているのかをTableの情報を使って解説します。こんな調子で、単純なFCC構造を説明するのに、図を含めて4ページ使っています。 記述のあちこちで、this is useful for physicists and chemists. といった文が見られます。こういう視点の本って、日本語ではなかなかありません。 今野さんの本にしてもこの本にしても、豊富な具体例で説明してくれる点がポイントです。多くの教科書にあるような数学として厳密な説明をいくら眺めても、「群論が物理現象理解にすげえ役に立つ」という実感を得るのは難しいでしょう。よほど数学がすきな人以外は、やるだけ無駄です。 |
ここでは今野さんのテキストなどをもとに勉強してやっと理解できた、空間群の情報をまとめてみました。
(ブラべー格子14×点群32)+(ブラべー格子×(回転、鏡映操作+部分的な並進操作))=「空間群 230個」
|
空間群の国際表記(P4/mbm, Fm3mなど)の意味
Λαβγ:
Λ:ブラべー格子の指定(P,I,F,A,B,C,R) α:主軸回りの対称操作([001]軸) β:主軸とは異なる軸回りの対称操作(立方晶なら[111]、正方晶なら[100]) γ:さらに別な軸回りの対称性(正方晶、立方晶なら[110]) その結晶構造の対称操作に、らせんやグライドなどの平行移動操作が含まれない場合は、αβγは点群の表記と一致する。 低対称構造で主軸以外に対称操作がない場合は、β、γは省略される。(P1とか) |
|
|
ブラべー格子: P:単純 A,B,C:底面心、側面心 F:面心 I:体心 R:菱面体 |
対称要素: 1,2,3,4,6:回転軸 m:鏡映面(2回回反軸と等価) 21:2回らせん軸 42:4回らせん軸 a, b, c:軸グライド面(軸方向に1/2並進して鏡映) n:対角グライド面 d:ダイアモンドグライド面 -:反転 4/m:4回軸があり、かつそれに垂直な鏡映面(m)がある。 4/n:4回軸があり、かつそれに垂直なn-glide面(n)がある。 mは-2と等価だから、3/mという要素は存在できない。 |
|
結晶学での面や軸などの表記法のルール |
|
| u,v,w | 格子点の座標 |
| [u v w] | 原点と格子点u, v, wを結んだ線(晶帯線)の方向を示す指数 |
| 〈u v w〉 | 同型の晶帯線の指数 |
| (h k l) | 結晶面の指数 |
| h k l | ブラッグピークの指数 |
| {h k l} | 同型の面の組の指数 |
空間群から斜方晶とか正方晶を見分ける方法
|
対称性の高い方から考えます。 立方晶: Fm-3mのように、対称要素の2番目に3または-3がくると立方晶。 正方晶: P4/mbmのように、最初に4か-4がくると正方晶。 六方晶: P621のように、最初に6か-6がくると六方晶。 三方晶: P322のように、最初に3か-3がくると三方晶。 直方晶: 上のどれでもなく、かつCmm2のように対称要素が3つあれば斜方晶。(mとmと2の3つ) 単斜晶 上のどれでもなくて、かつP2/mのように主軸だけが対称操作をもち、かつ2のやつ。 三斜晶 P1とP-1 斜方晶は、かならず対称要素が3つあるんだ。気づかなかった。正方晶では3つあるとはかぎらないな。 |
以下の説明でつかった結晶構造の3D図は、門馬さんと泉先生が開発したVICS-II をつかって作成しています。
実例で説明しましょ | |
|
P4:(正方晶) P = Primitive lattice(センタリングがない。) 4= 主軸( [001]軸)が4回対称をもつ。 でも、βとγの位置に記号がついていないから、[100]軸にも[110]軸にも対称操作はない。[001]軸まわりの4回対称だけってこと。 センタリングの説明 |
青原子は(000)位置、赤原子は一般位置(xyz) |
|
P4/mbm:(正方晶) P = Primitive lattice(センタリングがない。) 右図をみると底面心構造(C)な気がするかもしれませんが、単純格子です。コーナーと底面心で赤原子の向きがすこしちがいます。 4/m= 主軸( [001]軸)が4回対称をもち、かつ主軸に垂直な鏡映面がある。 b = [100]軸に垂直なbグライド面がある。(b軸方向に1/2b並進した後、[100]に垂直な面で鏡映する操作) m = [110]に垂直な鏡映面がある。(同時にその[110]が2回軸になっている。) (P4とmbm、じゃないんですよ。) 正方晶は4回対称があるため[100]と[010]は完全に等価になりますから、[100]の性質だけ表せば充分。あとは[110]の性質を記述すれば完成、という順番。 省略せずに書くと P 4/m 21/b 2/m |
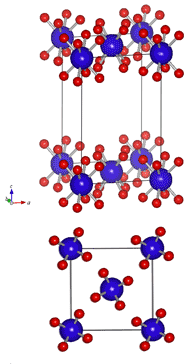
|
|
Fm-3m:(立方晶) F = Face centre lattice(原点から面心への3つのセンタリングがある。) m= [100]軸に垂直な鏡映面がある。(あからさまには見えないが実は[100]は4回対称軸にもなっている) -3 = [111]軸が3回回反対称(三回対称×反転操作)を持つ。 m = [110]に垂直な鏡映面がある。 立方晶は定義として必然的に[111]回りに三回対称または三回回反対称があるので、2番目に常に3か-3を表記する。逆に2番目が3か-3ならかならず立方晶。 省略せずに書くと F 4/m -3 2/m |
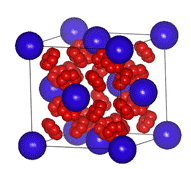 立方晶は対称性が高いので、一般位置の赤原子がうじゃうじゃと現れます。 |
|
Pnma:(斜方晶) P = Primitive lattice n = [100]軸に垂直なn-glide面(対角グライド面)がある。 m = [010]軸に垂直な鏡映面がある。 a = [001]に垂直なa-glide面がある。 斜方晶の場合、主軸をどれにとるかで混乱する場合があります。同じ物質なのに、論文によって主軸の取り方が異なっていて、そのため空間群が違っていたりする場合が結構ありますから、注意が必要です。 ありがたいことに、International Tableには、斜方晶で軸の取り方と変えるとどの空間群にかわるか、という一覧表があります。論文の軸の取り方と見比べてみれば、どう変換されるかすぐにわかると思います。 |
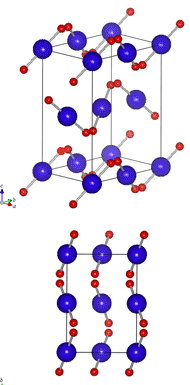
|
|
対称操作自身も、別の対称操作によって変換され、またある対称操作から自動的に別な対称操作が発生する場合もあるので、結局、国際表記に含まれる対称操作の情報だけですべての対称操作を作る事ができる(らしい)。 つまり、P4/mbm, Fm3mはただの名前ではない!! | |
センタリング結晶全体の平行移動 |
|
点群と異なり、結晶の空間群の場合は並進移動の操作が含まれます。特に、結晶全体を平行移動させて構造を一致させる事ができる操作があり、その操作をセンタリングとよびます。センタリングで重要なのは、すべての原子について下の平行移動をした先に同じ原子が存在することです。センタリングの名称はブラべー格子の名前と同じですから、空間群の最初に表記されています。 Iセンタリング コーナーから 体心位置への平行移動がひとつ (000) + (1/2,1/2,1/2) Fセンタリング コーナーから 面心位置への平行移動が3つ (000) ,+ (1/2,1/2,0) ,+ (1/2,0,1/2,) ,+ (0,1/2,1/2) Cセンタリング コーナーから底面心位置への平行移動がひとつ (000) ,+ (1/2,1/2,0) Aセンタリング コーナーから側面心位置への平行移動 (000) ,+ (0,1/2,1/2) 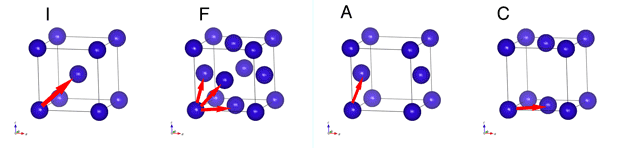
IとFで体心構造と面心構造ができます。Pはセンタリングがない構造(単純格子)で、平行移動では結晶をかさねる事はできません。 A,Cセンタリングは立方晶、正方晶、斜方晶にはありません。 六方晶、三方晶にはセンタリングをもつ構造はありません。 |
体心構造とか面心構造とか
|
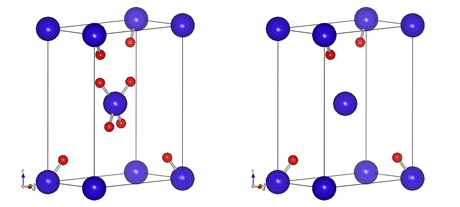
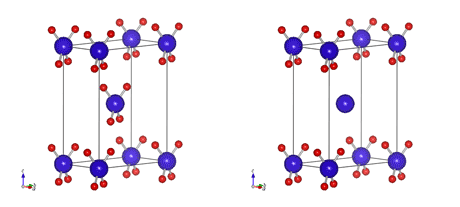
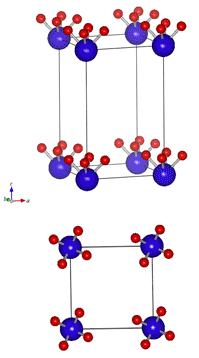
質問:下の二つの斜方晶構造は、体心格子構造でしょうか?ただし、赤い原子はユニットセル内にあるものだけを書いています。 どちらも体心構造にみえますか?実は、左は体心格子構造ですが、右は違います。単純格子です。これは単なる分類、呼び方だけの話ではなく、それぞれの原子の性質に深く関係する本質的な差ですから、ごちゃごちゃにしてはいけません。体心構造かどうかは、体心位置に原子があるかどうかではなく、コーナーと体心位置が等価になっているかどうか、で決まります。 下の図は、同じ構造をそれぞれ表示範囲を少し広げて書いた図で、こうすると体心の意味が分かると思います。(なんかバボちゃんが整列してるみたいだ。) 左図の構造は空間群I222で、右図はP222です。左図の構造では、体心位置のクラスターとコーナーのクラスターが同じ構造をしています。このため、左図のユニットセルを平行移動させてコーナー位置の原子が体心位置にくるようにすると、ぴったりかさなります。一方、右図では体心の青原子周りに赤原子がいませんから、体心位置の青原子とコーナーの青原子ではまわりの構造が異なっています。 左の構造の場合、コーナーと体心では構造に関する環境は完全に同じです。平行移動で完全にかさなるのですから、どこをコーナーにとるかは人間の勝手であり、性質が同じなのは当たり前ではあります。一方、右の構造の場合、コーナーと体心位置では、まわりの環境が異なっています。したがって、右図の構造をとる場合、コーナーと体心位置では、たとえ同種原子であっても性質が異なっています。 この差は重要です。たとえば、希土類の体心構造物質ならば、コーナーの希土類原子と体心位置の希土類原子の波動関数は一致していないといけませんが、右の構造の場合は、コーナーと体心で波動関数は一般には異なります。つまり、見た目はにていても、体心構造かそうでないかで、物質の物性が大きく変わります。決して呼び方の問題ではありません。 左図の構造は空間群I222で、右図はP222です。Iはこの構造が体心格子であることを、Pは単純格子である事を意味します。International Tableのそれぞれの場所の右ページをみると、I222ではGeneral Positionの上に +(000), +(1/2,1/2,1/2) と書いてあります。これは、I構造(体心構造)の場合、ある位置に原子があると、かならず(1/2,1/2,1/2)ずれた位置に同じ原子が存在している事を意味しています。たとえば(000)にDyがあれば(1/2,1/2,1/2)にもDyがなければいけません。すべての原子についてこの関係がなりたちますから、ユニットセル全体を+(1/2,1/2,1/2)だけ平行移動してぴたりと重なります。 一方、単純格子の場合は、Interantion tableにはこのような表記がありません。つまり、平行移動ではかさなることがありません。P222では(000)位置をとるサイトと(1/2,1/2,1/2)位置をとるサイトがあり、両方のサイトを同じ原子が占める事もありますから、ちょっと目には体心構造にみえます。しかし、それはたまたま別なサイトを同じ原子が占めただけで、それぞれの原子の物理的性質は異なります。おかれた環境がコーナーと体心位置で異なるのですから、当然です。 ここでは体心構造だけで説明しましたが、面心構造(F)、底面心構造(C)、側面心構造(A)でも同じ事です。体心構造(I)での+(1/2,1/2,1/2)のような平行移動をセンタリングといいます。センタリングがあるかないかで、一見似たような構造をもつ物質でも、物性が大きく異なります。 |
反転対称(4回回反)
|
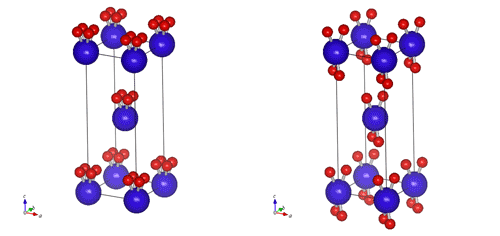
反転対称(正方晶なので4回回反)があるかないかの違い。体心位置が反転中心になっている。(体心構造なので、もちろんコーナーも) 反転対称で大事なのは、もし反転対称がないと、左図(I4)のように上下に向きがついてしまう事です。右図(I-4)でも体心位置で反対に入れ替えると構造が変わるようにみえますが、ひっくり返した後c軸のまわり90度回転させれば同じ構造になりますから、上下は等価です。向きがある構造と向きのない構造で、物性が大きく変わるのは当然です。反転対称がない、という性質は、たとえば誘電体での分極を考えるときに決定的に重要になります。 |
鏡映操作と反転操作の関係あからさまには現れない対称操作 |
|
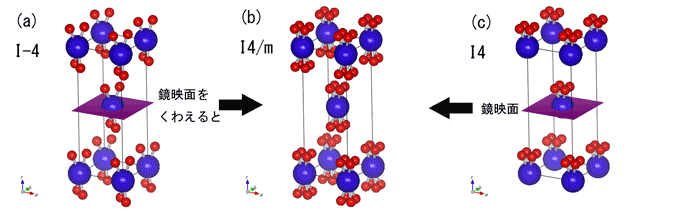
左(a)図は、上にもでてきた正方晶I-4構造です。体心位置を対称中心とした反転対称があります。で、この構造のc軸に垂直な鏡映面をz=1/2に置くと、その鏡映操作によって、中央(b)図の構造が生じます。この構造の空間群はI4/mです。この4/mとは、約束事として、四回軸がありかつその四回軸に垂直な鏡映面がある、という意味です。正方晶では、この四回軸をc軸にとります。もともと(a)に反転対称があるのですから、当然(b)の構造にも反転対称があります。 一方、右の(c)図はI4構造で、反転対称がありません。これに同じように紫の鏡映面による鏡映操作を加えて赤原子を移動させると、やはり中央(b)図の構造I4/mになるのがわかると思います。ポイントは、反転対称がない正方晶構造の体心位置に鏡映面を加えると、反転対称が生じる、という点です。 (b)図をながめていると分かると思いますが、四回対称軸(c軸)とそれに垂直な鏡映面が同時に存在する(つまり4/m)と、必然的に反転対称が生じています。c軸まわりに180度回転させて鏡映操作すれば、反転対称と同じ位置にくるからです。4回対称で鏡映面があれば必然的に反転対称があるので、反転対称についていちいち断る必要がなく、だから反転対称をあからさまには表示せずに4/mとだけ表記するようになります。また、(b)図でわかるように、I4/m構造ではa軸が二回対称軸になっていますが、それも四回対称と鏡映操作からの必然なので、やはり二回軸の事は表記しません。だから、空間群の表記に、ある対称操作が明示されていないからといって、その操作が含まれていないわけではありません。明示されている対称操作から必然的に生じるかくれた対称操作がある、という事をしっておく必要があります。 上の説明では、右(c)のI4に鏡映面を加えましたが、当然ですが、逆の言い方もできます。I4の体心位置に反転対称を加えると、やはり中央(b)図のI4/mになります。4回対称に鏡映を加えても、4回対称に反転対称を加えても、同じ対称操作になるからです。4回対称+反転対称で、4回回反にはならないんですね。 (う〜ん。2回対称で説明したほうがよかったかもしれない・・・・。) ところで (a)や(c)で、鏡映面はなんでz=1/2ときまっているのか、と疑問に思う人がいると思います。別なところにおいたら(b)の構造にならないではないか、と。 その疑問はもっともで、別なところにおいたら当然まったく別な構造になります。鏡映操作をくわえることで表れる複数の構造のうちの一つが(b)、というだけです。ただし鏡映面をどこにおくかでその後のユニットセルの大きさが変わります。ユニットセルの大きさを変えないためには、鏡映面が置ける場所は限定されz=0かz=1/2だけになります。 空間群を考えるとき、この気持ち悪さをよく感じますが、説明のために先に(b)の構造を示してから対称操作の話をしているために生じる混乱だと思います。本当は、正しい順番としては、元の構造とそれに新たに加える対称操作がまずあって、その結果どんな構造が生じるか、を考えることになります。 同様に、ユニットセルが先にきまっていてそこに対称操作を置いていくのではなく、すべての対称操作の結果、あるユニットセルが決定されます。 |
サブグループつまり対称操作の引き算、あるいは親子関係 |
上の説明は、I4やI-4に新たな対称性を加えてみると別な構造になる例で、いわば対称性のたし算です。たし算があるなら、引き算もあります。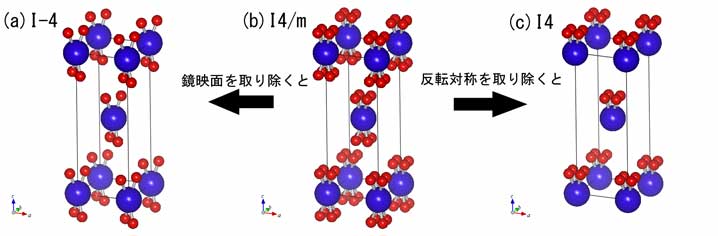
上の図で、中央(b)のI4/m構造は、4回対称だけでなく、鏡映面も反転対称もあります。で、このI4/mから反転対称をとりのぞくと、(c)のI4構造になります。一方、I4/mから鏡映面をとりのぞくと(a)のI-4構造になります。 おやぁ? I4もI-4も鏡映面を含まないので、単純にI4/mからの鏡映操作の引き算でかんがえるとI4とI-4の両方が答えになりそうです。でも、I4/mから鏡映操作をとりのぞいてもI4/mが持っていた反転対称は残っているので、I-4になります。たし算の例ではI4に鏡映面を加える事で生じたI4/mの反転対称ですが、できてしまえばI4/mの持つ鏡映面と反転対称は独立の操作で、I4/mから鏡映面を取り除いても反転対称は残ってしまいます。 さて、この話の何が重要かというと・・・ 構造物性研究では、構造相転移の理解が重要です。構造転移によりある物質の構造が低対称になるというのは、もとの構造がもっていた対称操作のどれかが失われる事、つまり対称操作の引き算がおきる事です。ですから物理現象としても、上のI4とI-4はI4/mと深い深いかかわりがあります。いわば親子関係でしょうか。I4/mより低対称の構造はたくさんありますが、この親子関係のため、特にI4とI-4をI4/mのサブグループとよび、他の空間群とはっきりと区別します。International Tableの核空間群の右ページ下にあるSubgroupとは、親切にも対称性の引き算の結果を全部書いてくれている表のことです。ちなみに、I4/mのSubgroupにはもうひとつI2/mもありますが、これはI4/mから四回対称をとったものです。 実際の研究でI4/mの構造をもつ化合物が構造転移を起こして低対称にうつった場合、その構造を考えるときには、まずはI4、I-4、I2/mの構造を当たってみることになります。もっとも自然はもう少し複雑で、サブグループのそのまたサブグループに落ちていったりしますが。 ところで、「サブグループとよぶ」などとカタカナでかいて、単なる分類の仕方のような説明をしましたが、そうではなくて、サブグループとはもちろん群論でいう部分群のことです。もともとI4/mを形成する対称操作は群をなしますが、そのI4/mの群から反転対称や鏡映操作をとりさった残りの対称操作もやはり群をなすので、それらはI4/mの部分群になっています。つまり空間群I4やI-4は、空間群I4/mの部分群です。だからサブグループ。あの抽象的な群論が、実はちゃんと自然を記述してるってわけです。不思議じゃありませんか? |
glide操作ってなにさ
|
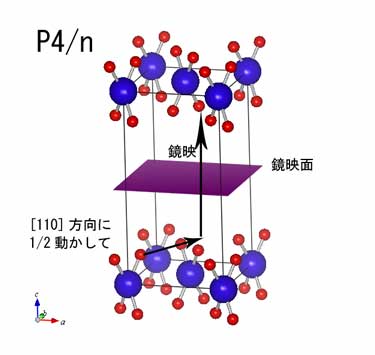
n-gilde(対角グライド)操作を例に。 下は、P4/n構造の図で、青原子は(000)位置、赤原子は(x,y,z)の一般位置にあります。P4/nとは、単純格子(P)で、[001]が4回軸になっていて(4)、かつ[001]に垂直なn-glide面(対角グライド面)がある(/n)構造、を意味します。 n-glide面を、左下コーナーでユニットセルの内側にある赤原子で考えてみましょう。[001]軸に垂直なn-glide面があるということは、まず赤原子を対角方向([110]方向)に(1/2,1/2,0)だけ並進移動し、それから[001]に垂直な鏡映面で鏡映操作します。その後、各方向にユニットセルひとつ分並進移動してやれば上の構造になります。 鏡映面はz=0に置いても等価な構造になります。この場合は、鏡映操作でユニットセルの下側にうつりますが、ユニットセル一つうごかせば図の矢印の先の赤原子と同じ位置にきます。 一方、青原子の場合、[110]方向に移動した後に鏡映操作しても、位置が変わらないか、等価な位置に移ります。したがって、n-glide操作しても(1/2,1/2,0)だけの移動と同じ位置、つまり底面心位置にきます。 平行移動を含みますが、基本的にはglide面は鏡映操作です。 n-glide面の他に、a-glide, b-glide, c-glideの軸glide面、ダイアモンドグライド面があります。名前(a,b,c,n,d)は移動させる方向を指定しています。bならばb軸方向に1/2移動させること、つまり+(0,1/2,0)だけ移動させる事を意味しています。 一方、鏡映面の置き方は、空間群の表記の何番目に置くかで指定します。 たとえば、空間群P4/mbmでは、2番目にbと書かれていて、これは[100]軸に垂直な鏡映面をおく事を意味しています。したがって、仮に3番目にbと書かれていれば、それは[110]に垂直な鏡映面がある、という意味です。 |
鏡映面と2回対称:あったりなかったりP422, P4mm,P4/mmの比較 |
|
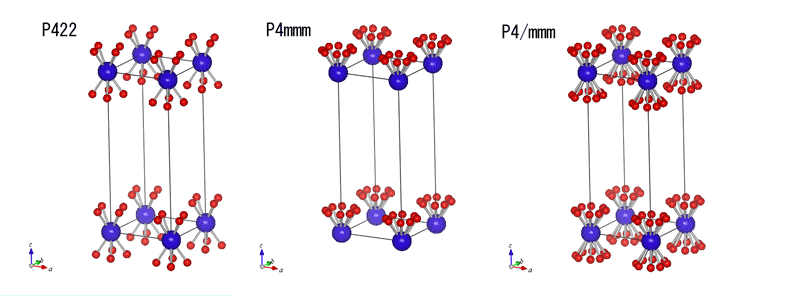
P422: [001]まわりに4回対称、[100]まわりに2回対称 、[110]まわりに別の2回軸、がある、という意味。 P4mm: [001]まわりに4回対称、[100]に垂直な鏡映面 、[110]に垂直な鏡映面、がある。 P4/mmm: [001]まわりに4回対称、かつ[001]に垂直な鏡映面、[100]まわりに鏡映面、[110]まわりに別の鏡映面、がある。 [001]周りに4回対称があるのが正方晶構造の定義です。それぞれの空間群の構造を下に書きました。青原子は(000)位置、赤原子は(xyz)の一般位置です。 下は[100]方向から見た図です。左図P422には、[001]に垂直な鏡映面がありません。でも[100]が2回軸になっているので、青原子位置や体心位置、それに(0,0,1/2)を通る[100]軸の周りで180度回転してやると、重なります。 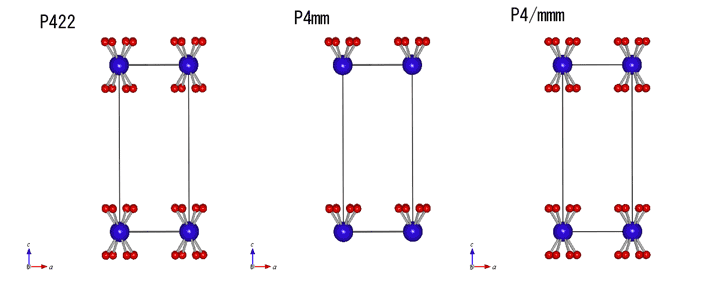
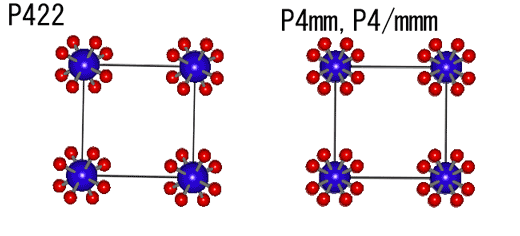
|
サイトシンメトリー
|
International Tableで、Wycoff letterの右に書いてあるやつ。 P4/mbmの2aサイトの場合なら 2 a 4/m.. 0,0,0 1/2,1/2,0 の4/m.. の部分。 このサイトに原子がある場合、その原子の位置を含む対称操作を書いてある。上の例だと、意味は: この原子位置には、主軸(c軸)と平行な4回対称軸が通っている。同時にこの原子を含み主軸に垂直な鏡映面がある 一方、2個のピリオド:..は [110][100]軸に関しては対称操作はない事を意味する。 General position(一番対称性の低いサイト。ITの一番上に書いてある)のようにすべての方向で対称操作がない場合は、1とのみ書かれる。 サイトシンメトリーは、このサイトの原子の上にのって結晶を見渡したときの結晶の点対称性でもある。 |
実例をみながらサイトシンメトリーを考える。
|
正方晶希土類化合物RB2C2の例 希土類のサイト:2a 4/m.. (0,0,0)(1/2,1/2,0) ボロンのサイト:4h m.2m (x,x+1/2,1/2) 炭素のサイト:4h m.2m (x,x+1/2,1/2) 希土類:4/m.. 右図をよく見ると、オレンジ色の希土類原子の位置では、c軸(主軸)は4回対称軸になっていて、かつ、希土類を含むc面が鏡映面になっている。 一方、B-Cリングが少しゆがんでいるので、希土類の位置では[100][110]軸には対称要素がない。つまり、希土類を通る[100][110]軸はどちらも回転対称軸ではないし、希土類を含んでかつ右図で画面に垂直な鏡映面がない。 ボロン・炭素のm.2m 右図を見ると、B-Cリングはz=1/2位置にあるので、BあるいはCを含むC面は鏡映面になっている。でも回転対称軸はない。だからm.2mの頭がm BあるいはCを通る[100]軸には対称要素はなにもない。だからm.2mの2番目が. 次は自信がない。 右図を見ると、あるB、Cを通る[110]軸のうちの1本は2回対称軸になっている。もう1本の[1-10]には回転対称はないが、[1-10]に垂直な鏡映面がある。 2dサイトの場合は:m.mm 2dサイトの位置は(0,1/2,0)と(1/2,0,0) RB2C2では実際には原子は存在しないけど、この位置のサイトシンメトリーを考える。 右図を見ると、[001]軸(主軸)については希土類と同じで、[001]に垂直な鏡映面がある。 この位置を通る[100]軸には対称要素はない。 問題はその次 右図を見ると、この位置を通る[110]軸に垂直な鏡映面がある。でも、それだとm.mだよなあ。m.mmになる意味が分からない。 |
RB2C2の構造(P 4/m b m:No.127)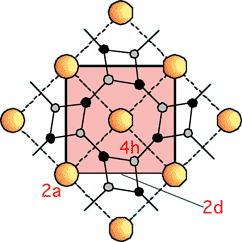 オレンジ:R(希土類):(0,0,0)(1/2,1/2,0) 黒:C:(x,x+1/2,1/2) 灰色:B:(x,x+1/2,1/2) ピンクがユニットセル |
Origin Choiceに注意
|
VENUS、RIETANを使う時は、Origin Choiceに注意しましょう。 230個の空間群のうちのいくつかは座標原点(Origin)の取り方が二つあり、Origin Choice 1, 2として両方がInternational table Aに載っています。Choiceがある場合は、Interrnational tableの右上、空間群番号の下に" Origin Choice 1"などと書いて有るので分かります。 どちらの表記も完全に等価ですが、座標の定義が変りますので、論文に載っていた位置パラメーターを使う場合にはどのOrigin Choiceを使っているのか注意が必要です。 Origin Choiceがあるのは次の空間群で、結構たくさんあります。 No. 5, 7, 8, 9, 12, 13, 14, 15: 48, 50, 59, 68, 70, : 85, 86, 88, 125,126, 129, 130, 133, 134, 137, 138,141,142,: 201, 203, 222, 224, 227, 228, 見分け方 論文で結晶の空間群と原子位置パラメーターが載っていたら、International Tableでその空間群のサイト情報を確認します。原子位置パラメーターがx=0.162などはんぱな実数になっている場合は、International Tableでのサイト座標が, x,x,xなど自由度のあるサイトを探します。x=1/4あるいはx=0.25など有理数になっている場合は、International Tableでのサイト座標が1/4,1/4,1/4などになっているものを探します。もし、論文に載っている原子位置座標がInternational Tableに載っていなければ、Origin Choiceが違っている可能性があります。International Tableで次のページにもう一つのOrigin Choiceのでの表示が載っているので、そこで同様にサイトを確認します。これで論文の原子座標が載っていれば、こちらのChoiceが正しいOriginです。 例えば、Fd-3m (No.227)の場合、最も対称性の良いサイトは8aサイトですが、その座標の表現は Choice 1: (0,0,0) (3/4,1/4,3/4) Choice 2: (1/8,1/8,1/8) (7/8,3/8,3/8) と、(当たり前ですが)Originで異なります。 VICS、RIETANでOrigin Choiceの指定と座標の表現に不一致があると、とんでもない結果になりますので、注意しましょう。VICSでは、Edit画面で空間群を指定する窓の下にsettingという窓があります。ここで1を選べばChoice1、2を選べばChoice 2になります。RIETANでは、空間群を番号で指定しますが、CHoice2を使う場合は、A-227-2というように空間群番号の後ろにChoiceをつけます。 なお、Originだけでなく、Unique Axisの取り方にも複数ある場合があります。 No.3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, また、Trigonalの場合は、Hexagonalの取り方とRhombohedralの取り方の二つがあり、どちらもInternational Tableにのっています。 論文にのっている結晶構造がどうにも変ならば、Internataional Tableの前後のページを良く見てみましょう。 |
立方晶の定義って?
|
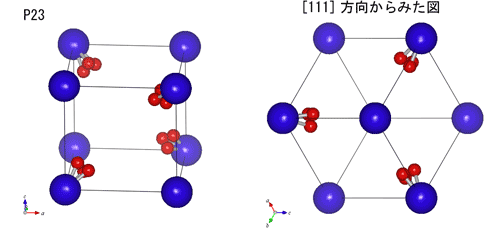
ときどき勘違いをしている人がいますが、対称性から見た立方晶の定義は、ユニットセルが立方体になっている事ではありません。4本ある[111]軸が全部3回軸になっていて、それぞれが同じ角度を成して交わっている事です。ですから、立方晶の空間群では、Fm-3mなどのように、点群の2番目に3回軸を表す3か-3が必ずついています。これは、3つの[100]軸の向きと長さが同じだけでは不十分で、完全に等価でないと立方晶とは言えない、ということを意味しています。 また、立方晶ならかならず4回対称がありそうですが、それも一般には間違いで、P23、I23などの対称性の立方晶では、4回軸は存在しません。 上の図は空間群P23の立方晶構造を書いたものです。青い原子は(000)位置、赤い原子は(x,y,z)の一般位置に入っています。左図の赤い原子をよく見れば、2回対称はあっても、4回対称がないのが分かります。じつはP23の2がそれを表しています。一方、この構造を[111]方向からみたのが右図で、三回対称の構造になっています。青原子を結ぶ線は[100][010][001]軸などで、この図で三回対称があるということは、[100][010][001]が完全に等価である事を意味しています。つまり立方晶です。 三方晶でも右図に見える方向がありますが、でも三方晶の場合はその方向は一つしかありませんから、区別できます。 立方晶で重要なのは3回対称であって、4回対称ではないのです。意外でしょ? |
座標系の取り方
|
The International TAbleでの図の座標軸は、右手系です。従って a軸: 図の下向き、 b軸:図の右向き c軸:紙面の外。 |
P-1に注意
| 空間群P-1(No.2)は、対称性が低いので、複数のユニットセルの取り方が許される。その取り方で、本質的にはP-1でも、I-1, F-1,C-1などの方が実際の物質の対称性を良く表現できる場合がある。特に、Fullprofの磁気構造の表記で使う。結晶構造がP系なら磁気構造にP-1を、FやI系ならF-1,I-1を使う。F-1、I-1などはInternational Tableに乗っていないけれど大丈夫、使えます。 |
International TableでのReflection Conditions(消滅則) |
|
International Tableには、それぞれの空間群、各サイトでのReflection Conditionsが全て記載されています。Reflection Conditions(反射条件)は時々消滅則と訳される事があるで、禁制反射(強度が0になる反射)のまとめみたいですが、逆で、禁制反射がある場合に反射が起きる条件を記載されます。私はこれを勘違いしていました。 General Condition その空間群をとれば、サイトシンメトリーに関係なく生じるReflection Conditions。あるいはGeneral PositionsでのRefelction conditions。 たとえばgeneral conditionが h00: h=2nだけだったら、「殆どの反射はみんな起きるが、a*方向(h00)に限り、200,400,600.......以外の反射は起きない。」という意味。だから、101や111反射なんかはちゃんとでます。「 h00: h=2nの反射は起きない。」とか「h00: h=2nの反射だけ起きる。」という意味ではありません。 Special condition 原子がGeneral Positions以外の高対称サイトに入っている場合、上のGeneral Conditionでの禁制則に加え、新たな禁制則(Extra condition)が生じる場合があります。その場合のそれぞれのサイトのReflection Conditionは、Specialとして、各サイトの右ふちに記載されています。 General Condition h00: h=2n 2aサイトのExtra condition が hh0;h=2n この意味は、「ほとんどの反射が生じるが、しかし元々(100)系では200,400,600.....のみ反射があり、さらに(2aサイトの原子からの散乱では)(110)系では220,440,660,....反射のみが起きる。」だから、110ブラッグはなくても、111ブラッグはある。 でも、 General Condition h00: h=2n 2aサイトのExtra condition が hh0;h=2n に加えて 8cサイトのExtra condition が no extra condition の場合、8cサイトでは、General Condition以外に消滅則はない、という事。だから、もし2aサイトも8cサイトも原子が占めていると、2aサイトの原子からは110ブラッグはでないけれど、8cサイトの原子からは110ブラッグがあるので、全体としては、110ブラッグが観測される。 ちょっと妙な気がするかもしれないけれど、general conditionとExtra Conditionは重ならないので、ある空間群のどのサイトに実際の原子が入っていようが、General Conditionに変わりはなくて、でないものはでない。 |
結晶中の点群:
|
点群は無数にあるが、並進対称性と両立する点群は以下の32種類だけ。 | |||||||
| 三斜 triclinic | 単斜 monoclinic | 直方 orthorhombic | 正方 | 三方 trigonal | 六方 | 立方 | |
| 1 | 2 | 4 | 3 | 6 | 23 | ||
| -1 | -2=m | -4 | -3 | -6 | m3 | ||
| -1 | 2/m | 4/m | -3 | 6/m | 2/m -3 | ||
| 222 | 422 | 32 | 622 | 432 | |||
| mm2 | 4mm | 3m | 6mm | m3m | |||
| m2m | -42m | -3m | -62m | -43m | |||
| 2/m2/m2/m | 4/m 2/m 2/m | -3 2/m | 6/m 2/m 2/m | 4/m -3 2/m | |||
| Cubicには4つの3回軸がかならずある。Cubicの点群の場合、この3を2番目に記述する。
2/m-3 => m3, 2/m2/m2/m => mmm, 4/m 2/m 2/m => 4/mmm, -32/m => -3m, 6/m2/m2/m => 6/mmm, 4/m -3 2/m => m-3m | |||||||